Area-Weighting: A Crude, Crude Alternative for Karl et al.

Dr. McKitrick and I have been having a nice discussion in the comments of my previous post criticizing his guest post at WUWT.  He has pointed out that the globally averaged buoy correction (originally from Kennedy et al. (2011B); see previous post for links) used in Karl et al. (2015) was applied without a consideration for area-weighting, and he is correct.  The global average was made by weighing each value according to observation count.  However, since most observations are from the northern oceans, this means that the global average, calculated as such, will naturally be close to the values in said regions.

This can be problematic because some values from other large regions, such as the tropical Indian or Southern Pacific, have pretty high correction values, roughly double the global value given by Kennedy et al.  What more, the standard deviations from each region are pretty comparable (excluding the Southern Ocean).  So an alternative global measure could be to attempt some crude, crude area weighting for each value, and then come up with a global value that way.


There are a couple pretty important obstacles to making this better than crude, crude.  First, Kennedy et al. do not seem to specifically define their regions, and I can't find any source online that gives the areas of the ocean regions anyway.  Whole oceans, yes; northern/southern, mysteriously no.  Second, I don't actually have a map available to me of the specific distribution of the buoys anyway, so how are they distributed within the ocean regions?  McKitrick suggested they are biased to shipping lanes; I have not double checked this, but if I'm pointing out obstacles then let's accept that on face value.

So a crude, crude alternative would go something like this.

1. Assume the oceans are roughly evenly divided between north, south, and tropical regions.  Further, where needed, assume west/east take equal areas.
2. Assume that the measurements for each region are uniformly distributed in the regions.

Neither assumption is correct of course, but again this is crude to provide what is a potentially more accurate number than 0.12˚C.

For the Pacific, Atlantic, Indian, and Southern Ocean areas, we have 165.2, 106.4, 73.56, and 20.33 million square kilometers, respectively.  So, to calculate a crude, crude area average:

where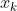 is the correction for the k-th region as they are listed in Table 5 of Kennedy et al., and 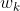is the area-weight for the k-th region.  Using this method, I obtained a global average of 0.146, contrasted to the correction of 0.121 that Kennedy et al. obtained by weighing according to sample size.

For standard error calculations, we can use the variance formula for propagation of error, using the standard error values for each region (the function f in that equation is the function written out above).  With that, I obtain a standard error of 0.012, for a mean value with 95% confidence bound of 0.146 ± 0.024˚C.  This does not estimate the uncertainty from the obstacles I named before.

This is a larger correction than the one Karl et al. applied; it is also incorrect, for the reasons I gave above.  All the same, the samples from the Northern Atlantic and Pacific oceans seem to be on the low side when you look at a more global picture.  I think this provides a crude, crude alternative value that area-weighs the measurements, which is going to be a more appropriate way of calculating a global average.